Skip to contents

The beta-binomial distribution.

Source: R/betabinom.R
BetaBinomial.Rd

Density, distribution function, quantile function and random generation for the beta-binomial distribution with parameters size, prob, theta, shape1, shape2. This distribution corresponds to an overdispersed binomial distribution.

Usage

dbetabinom(x, size, prob, theta, shape1, shape2, log = FALSE)

pbetabinom(
  q,
  size,
  prob,
  theta,
  shape1,
  shape2,
  lower.tail = TRUE,
  log.p = FALSE
)

qbetabinom(
  p,
  size,
  prob,
  theta,
  shape1,
  shape2,
  lower.tail = TRUE,
  log.p = FALSE
)

rbetabinom(n, size, prob, theta, shape1, shape2)

Arguments

x, q

Vector of quantiles.

size

Number of trials.

prob

Probability of success on each trial.

theta

Aggregation parameter (theta = 1 / (shape1 + shape2)).

shape1, shape2

Shape parameters.

log, log.p

Logical; if TRUE, probabilities p are given as log(p).

lower.tail

Logical; if TRUE (default), probabilities are \(P[X \le x]\) otherwise, \(P[X > x]\).

p

Vector of probabilities.

n

Number of observations.

Value

dbetabinom gives the density, pbetabinom gives the distribution function, qbetabinom gives the quantile function and rbetabinom

generates random deviates.

Details

Be aware that in this implementation theta = 1 / (shape1 + shape2). prob and theta, or shape1 and shape2 must be specified. if theta = 0, use *binom family instead.

See also

dbetabinom in the package emdbook where the definition of theta is different.

Examples

# Compute P(25 < X < 50) for X following the Beta-Binomial distribution
# with parameters size = 100, prob = 0.5 and theta = 0.35:
sum(dbetabinom(25:50, size = 100, prob = 0.5, theta = 0.35))
#> [1] 0.3054911

# When theta tends to 0, dbetabinom outputs tends to dbinom outputs:
sum(dbetabinom(25:50, size = 100, prob = 0.5, theta = 1e-7))
#> [1] 0.5397943
sum(dbetabinom(25:50, size = 100, shape1 = 1e7, shape2 = 1e7))
#> [1] 0.5397944
sum(dbinom(25:50, size = 100, prob = 0.5))
#> [1] 0.5397945

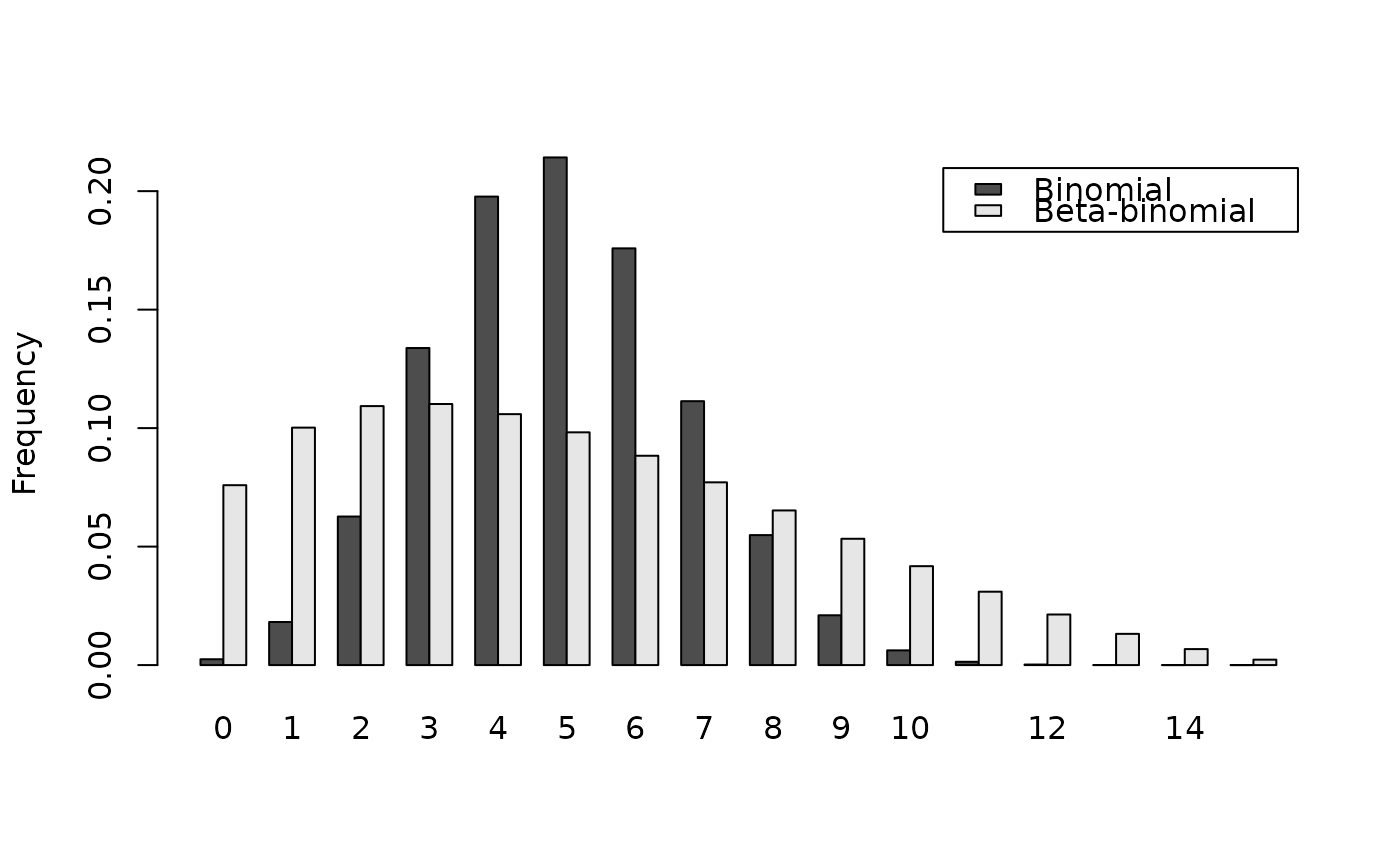
# Example of binomial and beta-binomial frequency distributions:
n   <- 15
q   <- 0:n
p1  <- dbinom(q, size = n, prob = 0.33)
p2  <- dbetabinom(q, size = n, prob = 0.33, theta = 0.22)
res <- rbind(p1, p2)
dimnames(res) <- list(c("Binomial", "Beta-binomial"), q)
barplot(res, beside = TRUE, legend.text = TRUE, ylab = "Frequency")


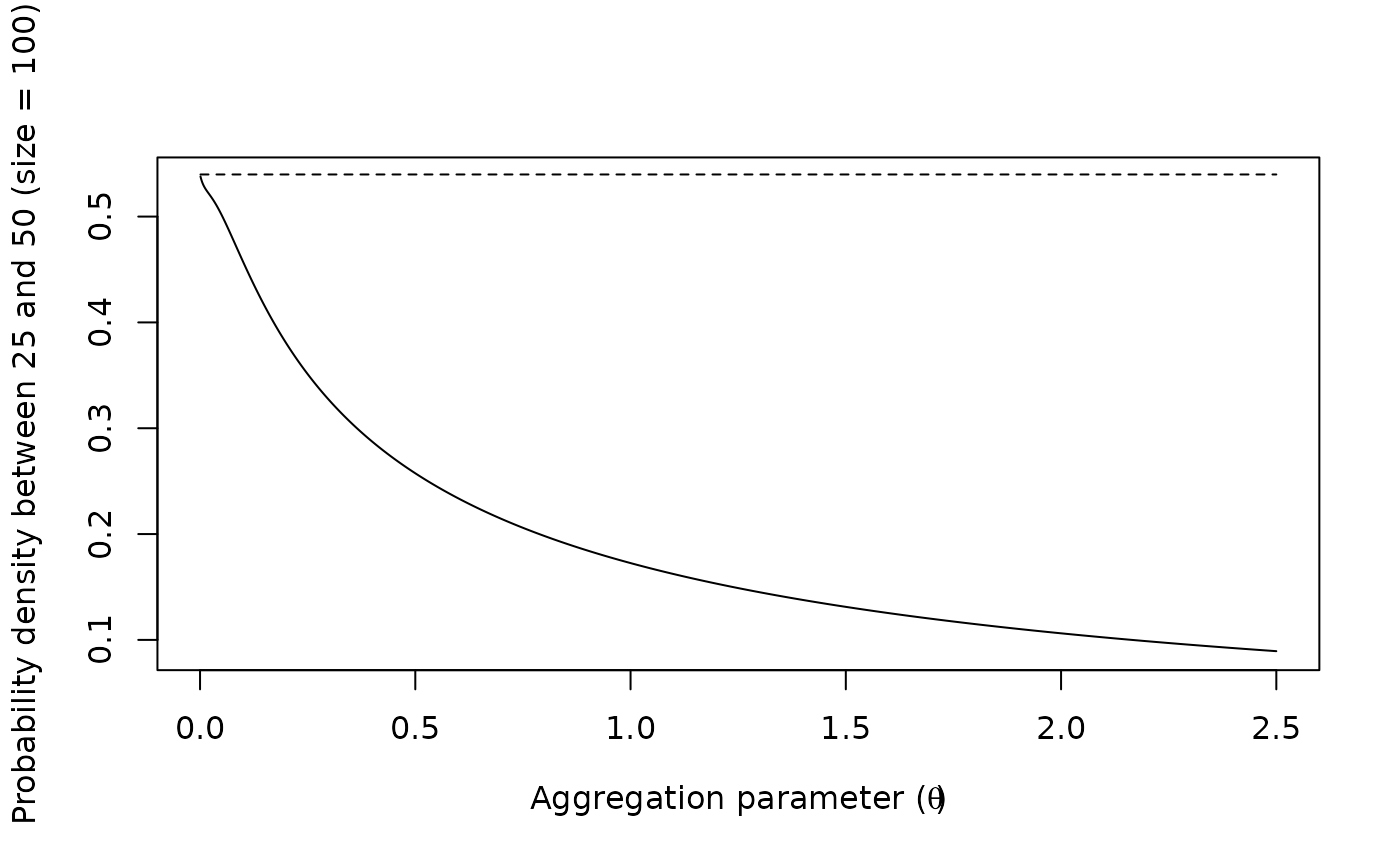
# Effect of the aggregation parameter theta on probability density:
thetas <- seq(0.001, 2.5, by = 0.001)
density1 <- rep(sum(dbinom(25:50, size = 100, prob = 0.5)), length(thetas))
density2 <- sapply(thetas, function(theta) {
    sum(dbetabinom(25:50, size = 100, prob = 0.5, theta = theta))
})
plot(thetas, density2, type = "l",
     xlab = expression("Aggregation parameter ("*theta*")"),
     ylab = "Probability density between 25 and 50 (size = 100)")
lines(thetas, density1, lty = 2)